Unit 2 - Exploring Two-Variable Data

 

Topic 2.1 Introducing Statistics: Are Variables Related?

Topic 2.2 Representing Two Categorical Variables

Topic 2.3 Statistics for Two Categorical Variables

Topic 2.4 Representing the Relationship Between Two Quantitative Variables

Topic 2.5 Correlation

Topic 2.6 Linear Regression Models

Topic 2.7 Residuals

Topic 2.8 Least Squares Regression

Topic 2.9 Analyzing Departures from Linearity

 

TOPIC 2.1 Introducing Statistics: Are Variables Related?

1. Understanding Variation: Random or Not?

Explanation

In statistics, variation refers to the differences or changes in data. For example, if we measure the height of all students in a class, we will notice that not everyone is the same height there s variation. This variation can be random (due to chance) or not random (due to a specific cause). Understanding whether variation is random or not helps us determine if the results we see are reliable or just happened by chance.

Data Example

Imagine we roll a die 10 times and record the results:

These results show variation because the numbers are different. This variation is random because each roll of the die is independent of the others and is due to chance.

Real-World Example

Imagine a teacher notices that students who sit in the front row tend to get better grades. The teacher might wonder if this is due to something about sitting in the front (not random) or if it s just by chance (random).

2. Patterns and Associations: Random or Not?

Explanation

When we look at data, we might see patterns or associations, like a trend or relationship between two variables. However, it s essential to determine whether these patterns are meaningful (not random) or if they occurred by chance (random). Just because we see a pattern doesn t mean there s a real relationship.

Data Example

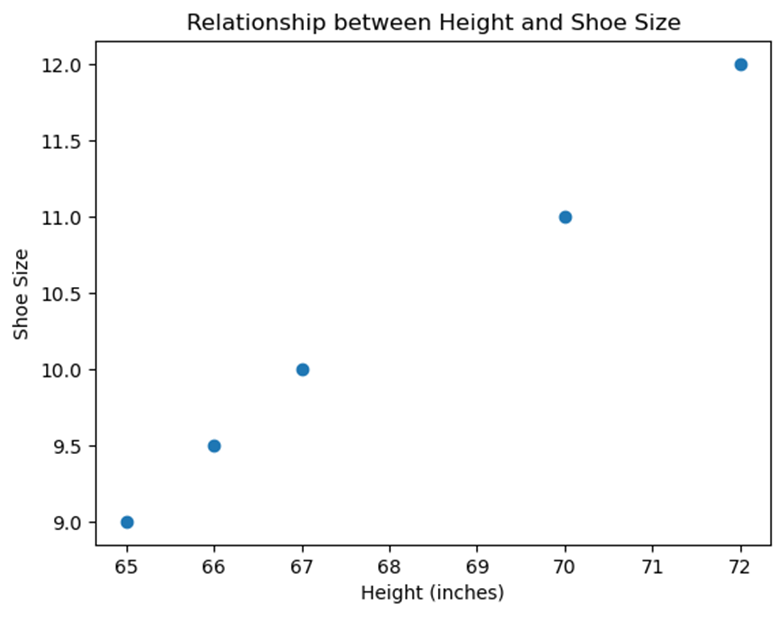
Let s consider the heights and shoe sizes of a group of students:

If we plot this data on a graph, we might see a pattern suggesting that taller students tend to have bigger shoe sizes. But is this pattern meaningful, or could it be random?

Graph

Graph showing the relationship between height and shoe size

Relationship between Height and Shoe Size

Real-World Example

A researcher observes that people who drink more coffee tend to have higher energy levels. However, this pattern might be random, or there could be another explanation, like people with naturally higher energy levels preferring coffee.

3. Identifying Questions: Possible Relationships in Data

Explanation

To analyze data effectively, we need to ask the right questions about possible relationships between variables. These questions guide our investigation and help us determine if what we observe is significant or just a coincidence.

Example Questions

Real-World Example

Suppose a school wants to know if there s a relationship between students attendance and their grades. They might ask, Does better attendance lead to higher grades? By asking this question, they can analyze the data to see if there s a meaningful relationship.

Free Response Problem

Question: A company wants to know if there s a relationship between the number of advertisements they run and the number of products they sell. Over ten weeks, they recorded the following data:

Week

Number of Ads

Products Sold

1

5

100

2

10

150

3

7

120

4

8

130

5

6

110

6

12

160

7

9

140

8

11

155

9

4

90

10

13

170

Task:

Answer Guide

This reading material should help you understand how to analyze data and recognize whether the patterns you see are meaningful or just random!

 

TOPIC 2.2 Representing Two Categorical Variables

Understanding Two Categorical Variables

1. Comparing Numerical and Graphical Representations

When working with two categorical variables, it's important to understand how to compare them using both numerical and graphical representations. Categorical variables are those that represent categories or groups, like "Gender" (Male, Female) or "Favorite Color" (Red, Blue, Green).

Numerical Representation: This is often done using a two-way table (or contingency table). This table shows how often different combinations of the categories occur. For example, if we survey 100 students about their gender and favorite color, a two-way table can summarize the responses.

Example:

Red

Blue

Green

Total

Male

15

10

5

30

Female

20

25

25

70

Total

35

35

30

100

Graphical Representation: To visualize the relationship between these two variables, we can use graphs such as side-by-side bar graphs, segmented bar graphs, or mosaic plots. Each of these graphs provides a way to visually compare the distributions of the categories.

2. Types of Graphical Representations

Let s dive into the three main types of graphical representations used for two categorical variables:

a) Side-by-Side Bar Graphs

In a side-by-side bar graph, bars for one categorical variable are placed next to each other, grouped by the categories of another variable.

Example: A side-by-side bar graph showing gender and favorite color might look like this:

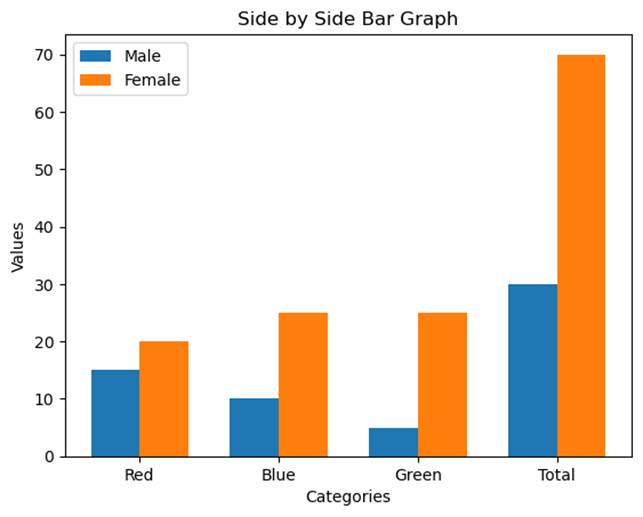
A graph with blue and orange bars Description automatically generated

b) Segmented Bar Graphs

In a segmented bar graph, each bar represents one category of a variable and is divided into segments that represent the categories of the second variable.

Example: A segmented bar graph for gender and favorite color:

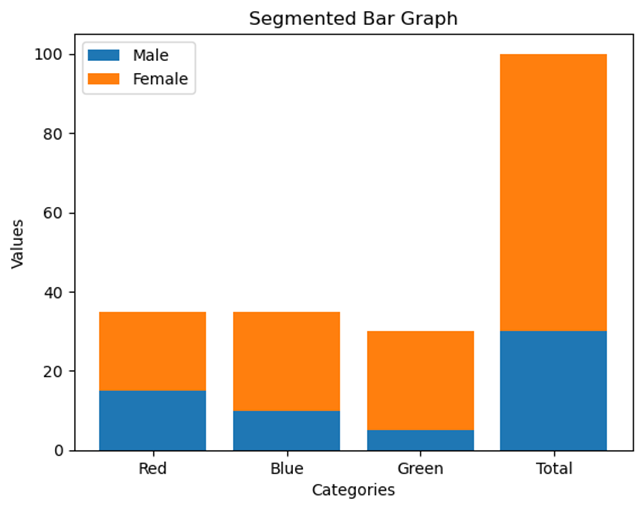
Segmented Bar Graph

c) Mosaic Plots

A mosaic plot is a graphical representation where the size of each rectangle is proportional to the frequency or relative frequency of that combination of categories.

Example: A mosaic plot for gender and favorite color:

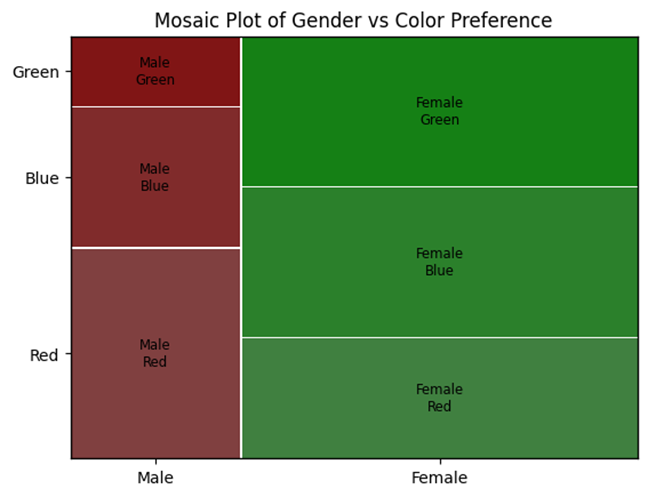
A mosaic plot of genders Description automatically generated

3. Comparing Distributions and Determining Associations

These graphical representations help us compare the distributions of two categorical variables and determine if there is an association between them.

4. Two-Way Tables (Contingency Tables)

A two-way table is a simple but powerful tool to summarize two categorical variables. The cells in the table can show frequency counts or relative frequencies (proportions).

Example: In the two-way table shown earlier, the cell for Male, Red shows a frequency of 15. If we wanted the relative frequency, we'd divide 15 by the total number of students (100), giving us 0.15.

5. Joint Relative Frequency

The joint relative frequency is found by dividing the frequency in a cell by the total number of observations. It tells us how often a particular combination of categories occurs.

Example: For the "Male, Red" category, the joint relative frequency is 15/100 = 0.15 or 15%.

Real-World Example

School Clubs and Sports Participation: Suppose we want to see if there is an association between students participating in school clubs and playing sports. We survey 200 students and create the following two-way table:

Plays Sports

Does Not Play Sports

Total

In a Club

60

40

100

Not in a Club

20

80

100

Total

80

120

200

These graphs help us see if being in a club is associated with playing sports.

Free Response Problem

Problem: A survey of 150 students asks about their favorite type of movie (Action, Comedy, Drama) and whether they prefer watching movies at home or in theaters. The data is summarized below:

Action

Comedy

Drama

Total

Watch at Home

30

20

10

60

Watch in Theaters

20

40

30

90

Total

50

60

40

150
  1. Create a side-by-side bar graph for the data.
  2. Calculate the joint relative frequency for students who prefer watching Action movies at home.
  3. Discuss whether there is an association between the type of movie and where students prefer to watch movies.

This reading material should give you a strong understanding of how to represent and analyze two categorical variables. Practice using these tools and graphs to strengthen your statistical skills!

 

TOPIC 2.3 Statistics for Two Categorical Variables

1. Introduction to Two Categorical Variables

In statistics, we often collect data that falls into different categories. When we study two categorical variables simultaneously, we can use a two-way table to organize and analyze the data. This allows us to observe patterns and relationships between the two variables.

2. Calculating Statistics for Two Categorical Variables

Let's start by understanding how to calculate basic statistics from a two-way table. A two-way table displays data that classifies individuals by two categorical variables.

Example:
Suppose we survey 100 students about their preferred study method (Group Study or Individual Study) and their grade level (Underclassmen or Upperclassmen). Here is the data:

Group Study

Individual Study

Total

Underclassmen

20

30

50

Upperclassmen

15

35

50

Total

35

65

100

 

3. Marginal Relative Frequencies

Marginal relative frequencies represent the proportion of individuals that fall into each category for one variable, without considering the other variable. They are calculated by dividing the row or column totals by the overall total.

A table with numbers and symbols Description automatically generated with medium confidence

This tells us that 35% of students prefer group study, while 65% prefer individual study. Similarly, 50% of the surveyed students are underclassmen, and 50% are upperclassmen.

4. Conditional Relative Frequencies

Conditional relative frequencies focus on a specific subgroup of the data. It s calculated by dividing the frequency of a cell by the total of its row or column.

A white background with black text Description automatically generated

These calculations help us understand the relationship between the variables.

5. Comparing Statistics for Two Categorical Variables

To compare statistics for two categorical variables, we analyze the marginal and conditional relative frequencies. For instance, by comparing the preferences for study methods between underclassmen and upperclassmen, we can see if there's an association between grade level and study preference.

6. Real-World Example: Voting Preferences

Imagine we want to understand voting preferences in a town based on age. We survey 200 people and ask them whether they prefer Candidate A or Candidate B. We also note whether they are under 30 or 30 and older.

Candidate A

Candidate B

Total

Under 30

60

40

100

30 and Up

50

50

100

Total

110

90

200

A screenshot of a math test Description automatically generated

This shows that younger voters are more likely to prefer Candidate A compared to older voters.

7. Graphical Representation

Let s visualize the data from our student survey:

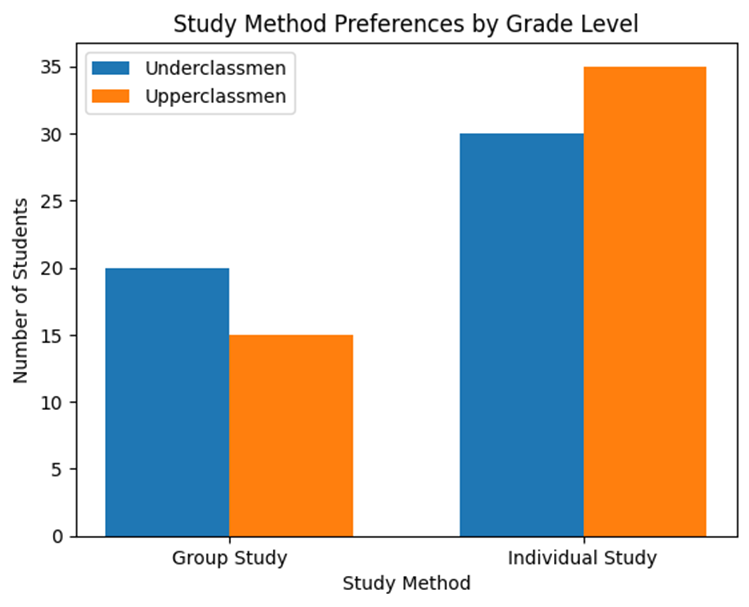
A graph of blue and orange bars Description automatically generated

8. Free Response Problem

Problem:
A company wants to understand whether employees' job satisfaction is related to their department. The company surveys 150 employees, recording whether they are satisfied or not, and whether they work in the Sales or Marketing department.

Satisfied

Not Satisfied

Total

Sales

40

35

75

Marketing

30

45

75

Total

70

80

150

Answer these questions and summarize your findings in a few sentences.

 

 

TOPIC 2.4 Representing the Relationship Between Two Quantitative Variables

1. What is Bivariate Quantitative Data?

Bivariate quantitative data involves observing two different quantitative variables for each individual in a sample or population. For example, imagine you collect data on the number of hours students study and their corresponding scores on a test. Here, "hours studied" and "test scores" are the two quantitative variables.

Data Example:

Let's consider a small dataset where we observe the hours studied and test scores for five students:

Student

Hours Studied

Test Score (%)

1

2

70

2

4

75

3

6

85

4

8

90

5

10

95

Here, "Hours Studied" is one variable, and "Test Score" is another. Together, they form a bivariate dataset.

2. What is a Scatterplot?

A scatterplot is a graph that represents bivariate data. Each point on the scatterplot corresponds to an observation in the dataset, with the x-axis representing one variable and the y-axis representing the other.

Example:

Using the data from our previous example, we can plot a scatterplot where "Hours Studied" is on the x-axis and "Test Score" is on the y-axis.

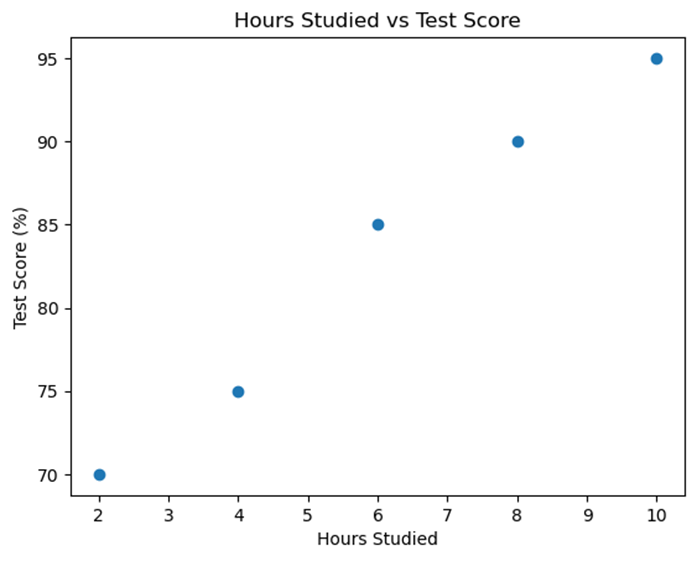
Scatterplot of Hours Studied vs Test Score

3. Explanatory and Response Variables

In a bivariate dataset, we often try to understand how one variable affects another. The explanatory variable (or independent variable) is the variable we use to explain or predict the other variable. The response variable (or dependent variable) is the one that we are trying to predict or explain.

Example:

In our example, we might want to see if the number of hours studied (explanatory variable) can help predict a student's test score (response variable).

4. Characteristics of a Scatterplot

When analyzing a scatterplot, we look for the following characteristics:

Example Analysis:

 

Regression Models and Predictions

Regression models are tools that help us understand and predict the relationship between two quantitative variables. By using these models, we can make predictions about the response variable based on changes in the explanatory variable.

Key Points:

  1. Purpose of Regression Models:
  2. Simple Linear Regression:

A white paper with black text Description automatically generated

  1. Making Predictions:

A math equation on a white background Description automatically generated

  1. Interpreting the Slope and Intercept:
  2. Limitations and Assumptions:

5. Real-World Example:

Let's consider a real-world scenario where a researcher wants to explore the relationship between the number of hours people exercise per week and their cholesterol levels. The researcher gathers data from 100 individuals and creates a scatterplot.

In the scatterplot, the x-axis represents the hours of exercise, and the y-axis represents cholesterol levels. If the scatterplot shows a negative direction, it might suggest that as people exercise more, their cholesterol levels tend to decrease, indicating a potential negative association between these two variables.

6. Free-Response Problem:

Problem:
A teacher gathers data on the number of hours students spend on homework each week and their corresponding GPA. The data for 10 students is as follows:

Student

Hours of Homework

GPA

1

3

2.5

2

5

3.0

3

7

3.5

4

4

3.0

5

6

3.2

6

8

3.7

7

2

2.2

8

9

3.8

9

10

4.0

10

1

2.0

This material provides a foundation for understanding how to represent and interpret the relationship between two quantitative variables using scatterplots. Use the data and real-world examples to guide your understanding, and try solving the free-response problem to practice your skills!

 

 

 

TOPIC 2.5 Correlation

Introduction

In statistics, correlation is a measure that describes the relationship between two quantitative variables. When we study how one variable changes in relation to another, we often look at the correlation to understand the strength and direction of this relationship. In this reading material, we will explore how correlation is calculated, how to interpret it, and some important considerations when using correlation in data analysis.

1. Regression Models and Predicting Responses

A regression model helps us predict the value of one variable (the response variable) based on the value of another variable (the explanatory variable). For example, if we have data on students study hours and their test scores, we might use a regression model to predict a student s test score based on how many hours they studied.

Data Example: Imagine you have the following data:

Study Hours

Test Score

2

70

4

80

6

90

8

95

A regression model might show that for every additional hour of study, the test score increases by a certain amount. This allows us to make predictions about future test scores based on study hours.

Real-World Example: Consider the relationship between the temperature outside and the sales of ice cream. A regression model could predict ice cream sales based on the temperature. As the temperature increases, ice cream sales might also increase, showing a positive relationship.

2. Determining Correlation for a Linear Relationship

Correlation quantifies the strength and direction of the linear relationship between two variables. The correlation coefficient, denoted as r, ranges from -1 to 1.

Graph Example: Let's create a scatterplot with two variables: study hours and test scores.

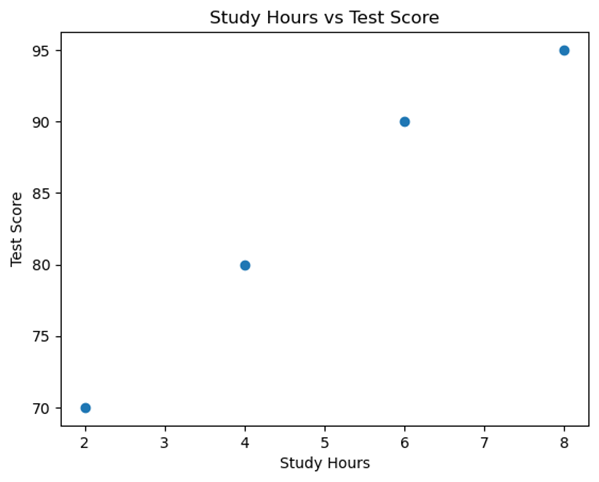
Study Hours vs Test Score

The scatterplot shows a positive linear relationship, meaning that as study hours increase, test scores tend to increase as well.

3. Understanding the Correlation Coefficient (r)

The correlation coefficient r tells us two things:

  1. Direction: Whether the relationship is positive or negative.
  2. Strength: How strong the relationship is (how close the points are to a straight line).

Example:

The closer r is to 1 or -1, the stronger the relationship. However, it s important to remember that a high correlation does not mean one variable causes the other to change.

4. Calculating the Correlation Coefficient

While the formula for calculating r involves some complex calculations, most often, we use technology (like a calculator or software) to find it. The formula is:

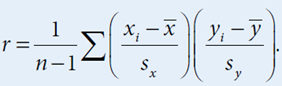
A mathematical equation with numbers Description automatically generated with medium confidence

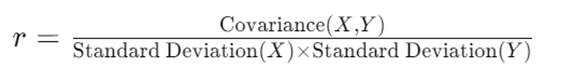
A black text on a white background Description automatically generated

5. Interpreting the Correlation Coefficient

When interpreting r, consider the following:

Example: Suppose r = 0.95 for study hours and test scores. This indicates a strong positive relationship, meaning that generally, students who study more tend to have higher test scores.

6. Correlation vs. Causation

A key concept in statistics is that correlation does not imply causation. Just because two variables are correlated does not mean that one causes the other to change.

Example: Imagine a study shows a correlation between ice cream sales and drowning incidents. This does not mean that buying ice cream causes drowning. Instead, a third variable (like hot weather) might cause both to increase.

Free Response Problem

Problem:
A researcher collected data on the number of hours spent exercising per week and the cholesterol levels of a group of adults. The correlation coefficient between the two variables was found to be r = -0.85.

Solution:

Conclusion Understanding correlation helps us explore and interpret relationships between variables. However, always remember the limitations of correlation and the importance of looking beyond the numbers to the context of the data.

 

TOPIC 2.6 Linear Regression Models

1. Understanding Linear Regression Models

A linear regression model helps us predict the value of a response variable y based on the value of an explanatory variable x. The relationship between x and y is modeled by a straight line, called the regression line. This line shows how changes in x are associated with changes in y.

2. The Regression Equation

A math problem with equations Description automatically generated with medium confidence

3. Calculating a Predicted Response Value

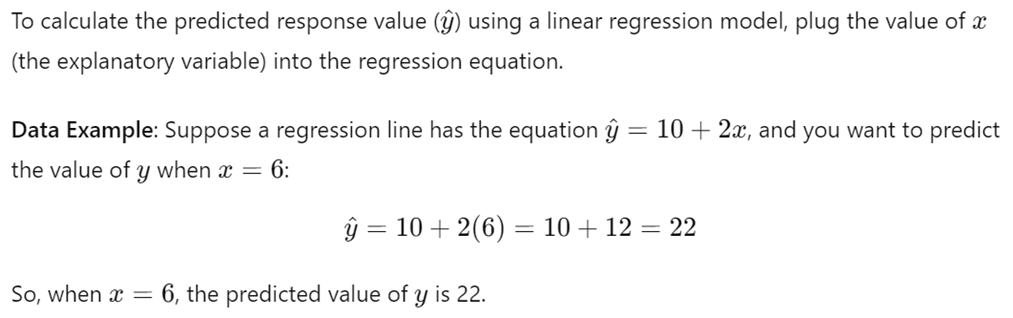
A math problem with numbers and equations Description automatically generated with medium confidence

4. Real-World Example: Predicting House Prices

A math equations on a white background Description automatically generated

5. Understanding Extrapolation

Extrapolation involves using the regression model to predict y for an x-value that is outside the range of data used to create the model. This can be risky because the further we go beyond the data we have, the less reliable the prediction becomes.

Example: If the house size data you collected ranges from 1,000 to 3,000 square feet, predicting the price for a 5,000-square-foot house using the same equation could lead to an unreliable estimate. The relationship might not hold true for such a large house.

6. Visualizing the Concept

Below is a graph of a simple linear regression model with a regression line:

Simple Linear Regression

TOPIC 2.7 Residuals

What Are Residuals?

In statistics, a residual is the difference between an actual observed value (y) and a predicted value (y^\hat{y}y^​) based on a regression model. Residuals help us understand how well our model fits the data. The formula for calculating a residual is:

Residual=85−90=−5

This means the student scored 5 points lower than predicted.

Residual Plots

A residual plot is a graph that shows residuals on the vertical axis and another variable (either the explanatory variable or the predicted response values) on the horizontal axis. Residual plots are a valuable tool for evaluating the fit of a regression model.

Interpreting Residual Plots

  1. Apparent Randomness:
  2. Patterns in Residuals:

Real-World Example: Predicting House Prices

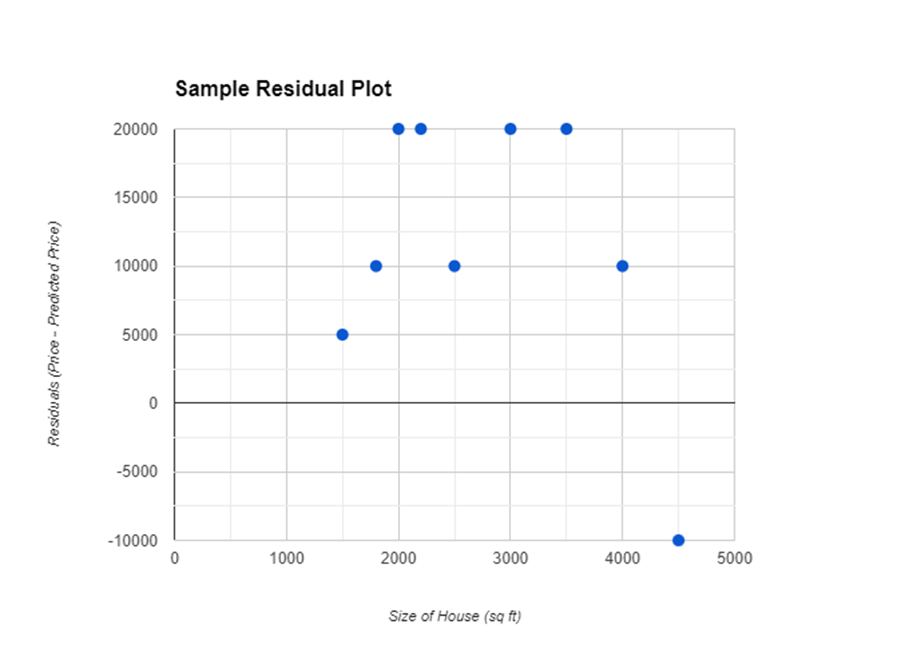
Let s say a real estate analyst is using the size of a house (in square feet) to predict its price. After building a linear regression model, the analyst calculates the residuals for each house in the dataset.

Here s a sample residual plot for better understanding:

A graph with blue dots Description automatically generated

Using Residual Plots to Evaluate Model Appropriateness

Residual plots help you decide if your chosen model is the best one for the data. If the residuals are random, your model is likely appropriate. If there s a pattern, you might need to explore different models.

Free Response Problem:

A company uses the number of years of experience to predict the salary of its employees. After fitting a linear regression model, they obtain the following data for three employees:

Employee

Years of Experience (XXX)

Actual Salary (yyy)

Predicted Salary (y^\hat{y}y^​)

Residual (y−y^y - \hat{y}y−y^​)

1

2

$50,000

$52,000

2

5

$70,000

$68,000

3

10

$100,000

$98,000
  1. Calculate the residuals for each employee.
  2. Create a residual plot by plotting the residuals against the years of experience.
  3. Interpret the residual plot. Does it suggest that the linear model is appropriate? Why or why not?

This reading material provides a clear and simple understanding of residuals, engaging students with explanations, examples, and a problem to solve.

 

TOPIC 2.8 Least Squares Regression

Introduction

In statistics, one of the most powerful tools we use to understand the relationship between two quantitative variables is the least-squares regression line. This line allows us to make predictions and understand how changes in one variable might affect another. Let's break down the key concepts of least-squares regression in a simple, engaging way.

1. Estimating Parameters for the Least-Squares Regression Line Model

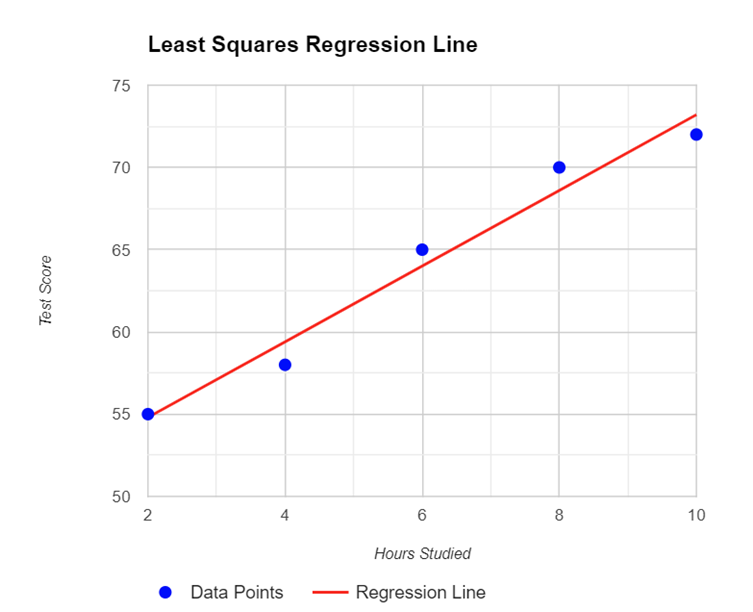
When we have two variables, say x (explanatory variable) and y (response variable), we often want to find the line that best fits the data points on a scatterplot. This line is called the least-squares regression line.

The parameters of this line include the slope and the y-intercept. These parameters help us understand how much y changes for a given change in x, and where the line crosses the y-axis.

Data Example: Suppose we have data on the number of hours studied (x) and the scores on a test (y) for a group of students. We want to find the line that best predicts the test score based on hours studied.

2. The Least-Squares Regression Model Minimizes the Sum of the Squares of the Residuals

The least-squares regression line is special because it minimizes the sum of the squares of the residuals. A residual is the difference between the observed value (y) and the predicted value (ŷ) from the regression line. By squaring these differences and adding them up, we get a value that the regression model tries to minimize.

This line also passes through the point (x̄, ȳ), where x̄ is the mean of the x-values and ȳ is the mean of the y-values.

A graph with a red line and blue dots Description automatically generated

3. Calculating the Slope (b) of the Regression Line

A white paper with black text and black text Description automatically generated

4. Interpretation of the y-Intercept (a)

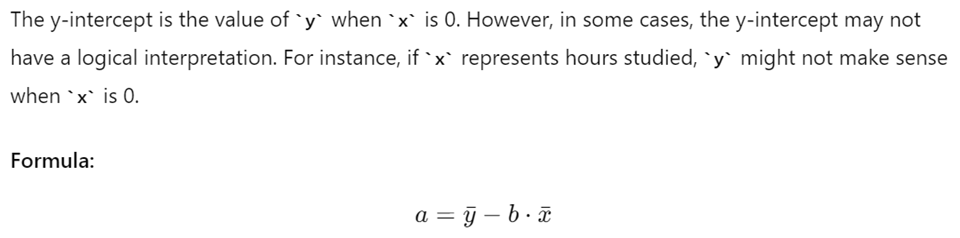
A white background with black text Description automatically generated

5. The Coefficient of Determination (r )

The coefficient of determination, denoted as r , is a measure of how well the regression line explains the variation in the response variable. It is the square of the correlation r and represents the proportion of variation in y that is explained by x.

6. Interpreting Coefficients of the Least-Squares Regression Line

The coefficients include the slope b and the y-intercept a. Understanding these coefficients helps us make predictions and understand the relationship between the variables.

7. Sample Calculation

A screenshot of a test Description automatically generated

A math equations on a white background Description automatically generated

A screenshot of a math equation Description automatically generated

This indicates that 98% of the variation in test scores is explained by the number of hours studied.

A graph with a red line and blue dots Description automatically generated

 

TOPIC 2.9 Analyzing Departures from Linearity

Introduction

When analyzing data using linear regression, it s important to recognize points that don't follow the general trend. These points can affect the overall regression model, leading to inaccurate predictions. In this lesson, we will explore how to identify influential points, understand outliers, and leverage points, and how to use transformations to improve our regression models.

1. Identifying Influential Points in Regression

Influential Points are data points that, if removed, significantly change the result of the regression analysis. These changes could affect the slope, y-intercept, or the correlation of the regression line. Outliers and high-leverage points are often influential.

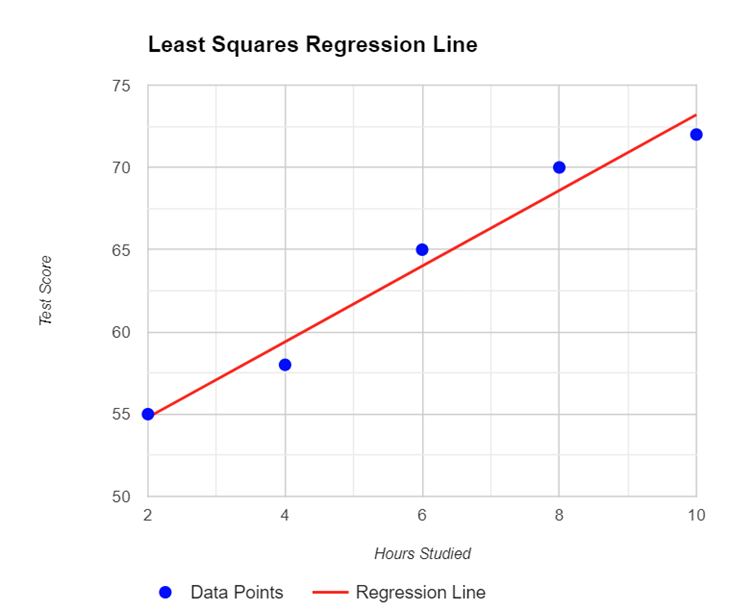
Example:

Imagine you have the following data set representing the relationship between the number of hours studied and test scores:

Hours Studied

Test Score

1

55

2

60

3

65

4

70

5

75

6

80

20

100

Here, the point (20, 100) could be an influential point because the x-value (20 hours) is much larger than the rest of the data points.

2. Understanding Outliers in Regression

Outliers are points that do not follow the general trend of the data and have a large residual when the Least Squares Regression Line (LSRL) is calculated. Residuals are the differences between the observed values and the values predicted by the regression line.

Example:

If you look at the same data set and plot the regression line, the point (20, 100) might be far away from the line, making it an outlier. This point will have a large residual because the actual test score is much higher than what the model would predict based on the other data points.

3. Understanding High-Leverage Points in Regression

High-Leverage Points have x-values that are much larger or smaller than those of other observations. These points can pull the regression line towards them, affecting the overall fit of the model.

Example:

In the previous data set, the point (20, 100) is also a high-leverage point because the x-value (20) is much higher than the other x-values (1-6). This point could strongly influence the slope of the regression line.

4. Understanding Influential Points in Regression

An Influential Point is any point that, when removed, changes the relationship between variables significantly. This change could affect the slope, y-intercept, and/or correlation of the regression line.

Real-World Example:

Imagine you're analyzing the relationship between advertising spending and sales revenue for a company. Most data points show that as advertising spending increases, so does sales revenue. However, one data point represents a situation where a significant amount was spent on a campaign, but the sales did not increase as expected. This point could be an influential point, especially if it drastically changes the regression line when removed.

5. Calculating a Predicted Response Using a Least-Squares Regression Line for a Transformed Data Set

Transforming data can help in fitting a more appropriate model when the original data does not follow a linear trend.

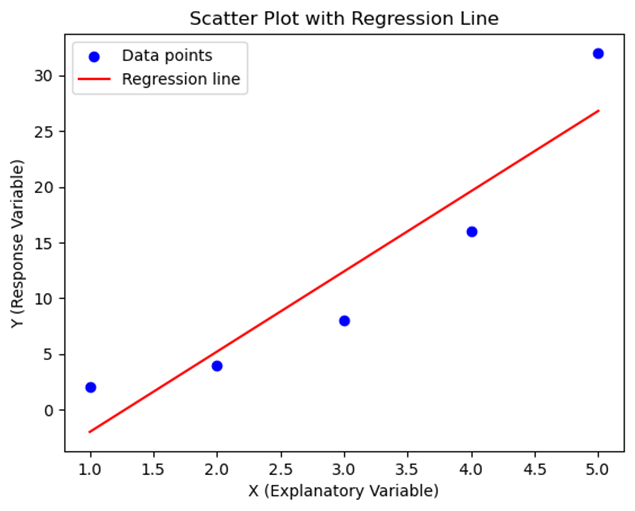
Example:

Suppose we have the following data set:

X (Explanatory Variable)

Y (Response Variable)

1

2

2

4

3

8

4

16

5

32

Here, the relationship between X and Y is exponential. By taking the natural logarithm of Y, we can transform the data to make it linear.

6. Transformations to Improve Linearity

By transforming variables, such as taking the natural logarithm of each value of the response variable or squaring each value of the explanatory variable, we can create transformed data sets that may better fit a linear model.

Example:

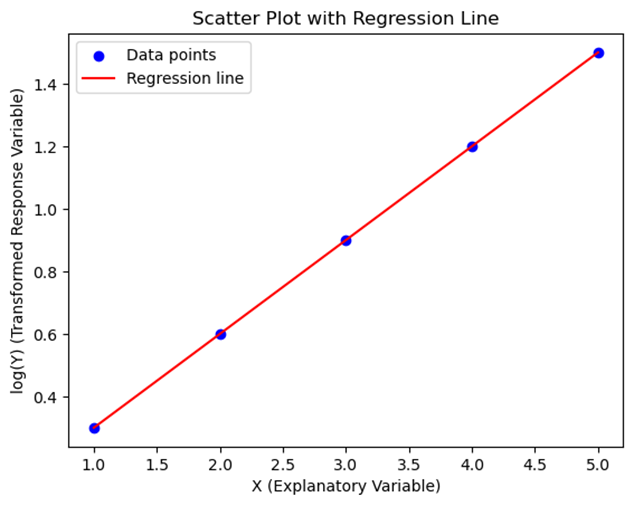
Using the previous data, we can create a new data set by taking the logarithm of Y:

X (Explanatory Variable)

log(Y) (Transformed Response Variable)

1

0.30

2

0.60

3

0.90

4

1.20

5

1.50

Now, the data follows a more linear pattern.

7. Interpreting Residual Plots After Transformation

After transforming data, we can analyze residual plots to determine if the transformation made the model more appropriate.

Graph:

Below is a graph that shows the original data points, the regression line before transformation, and the transformed regression line.

In this graph, the residuals for the transformed model are more randomly distributed, indicating a better fit.

Scatter Plot with Regression LineScatter Plot with Regression Line

Free Response Problem

Problem:

You have the following data set representing the number of hours spent on social media per day and the resulting productivity score out of 100:

Hours on Social Media

Productivity Score

1

90

2

85

3

75

4

65

5

60

6

55

15

50
  1. Identify any outliers, high-leverage points, and influential points in the data set.
  2. Transform the data set using the natural logarithm of the productivity score and plot the new data.
  3. Calculate the regression line for the transformed data and compare it with the original regression line.
  4. Discuss whether the transformation improved the model and explain why.

This reading material should help you understand how to identify and deal with influential points, outliers, and high-leverage points in regression analysis. By transforming data, you can often create more appropriate models that better predict outcomes.